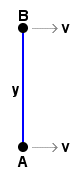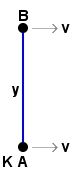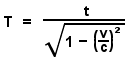The Relativistic Right Triangle
©J. Tanner - 2014 - Revised
The purpose of the triangle we are about to define in the following thought experiment is to compare the apparent path of a photon (light signal) as determined by two observers A and B with the same physical path as measured by a relatively static observer K, while they move past him in parallel at constant speed v, separated by constant distance y, from the point of view of observer K.
We will be observing the scene of the experiment as if looking down from an imaginary higher (3rd) dimension directly above the static ground plane.
The moving observers, A and B, are relatively static to each other and can ignore the motion relative to the ground with respect to their part in this experiment. Observers A and B share a common clock because they share a common, static frame of reference relative to each other, to which their clocks equally apply. In fact, we can consider their clock as being in between them and both of them using it as their common reference.
Observer K must take into account the movment of the photon between A and B
and their motion relative to him on the ground to define the physical photon path relative to his viewpoint. This is his part in this experiment.
A physical linear path will be defined starting where A released the photon to the point where B received it, as measured according to K. The length of this path will then be compared to the length of the same path according to A and/or B.
This means that observers A and B will contribute the vertical side (y) of the triangle, based on the passage of the photon between them, and that static observer K will contribute the horizontal (x) side, and the actual physical path of the photon will contribute the remaining diagonal side (R).
To make the comparative times required for the photon to traverse the path
between A and B distinguishable relative to static ground observer
K's time, the time as measured by A and B, is symbolized as
t and the time as reckoned by K, is symbolized as T.
All parties agree in advance as to the distance y which separates A and B, the speed of light, c, and the constant speed v, so these symbols may be shared in common without confusion or conflict. Initially, t and T are both equated to zero.
Defining the Sides of the Relativistic Right Triangle
 |
Two observers (A and B) are separated by constant distance y. To each other, they are relatively static, simply facing each other and remaining at the same distance apart.
Observer A sends a photon to B, which travels between them at speed c and takes time t = y/c. They both agree that the numerical value of y = ct. Since there is no motion for them to consider, other than the photon, the equation y = ct, fully defines the path of the photon and they agree on all the numerical quantities involved.
There is no reason for them to disagree with each other because they share the same identical frame of reference. |
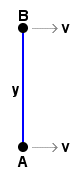 |
Now we will refer to a static ground plane just below A and B and they are traveling in parallel at constant speed v relative
to this static ground plane.
A and B still remain relatively static to one another and still agree as to all the quantities defining the light path between them. Nothing has changed for them. |
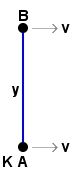 |
Another observer, K, is standing on the static ground plane as Aand B travel by at constant speed v relative to him, just barely above the ground.
A then sends another photon to B. To A and B, everything is still the same as before as pertains to the photon path. To them, defining the light path requires no reference to the static ground plane. |
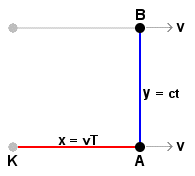 |
From the viewpoint of observer K, A and B
have both moved distance x along the ground since the photon was
released and according to K, this distance is x
= vT, according to his clock.
This x value refers to the distance
that A and B have moved relative to the static ground
plane while the photon passed between them as measured by K.
To observer K, on the static ground plane, these two motions must
be accounted for to define the same light path between A and B
with respect to the ground. |
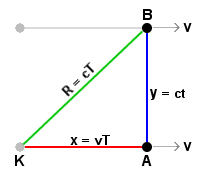 |
From
the static ground plane, the light path actually follows diagonal path R
when both the motion of the photon along y and the motion
relative to the static ground plane are taken into account.
The distance y, is also agreed upon by observer K, regardless of the motion along x. The distance is R = cT, according to observer K on the ground.
The motion of A and B relative to the ground, at speed v, is passed to the released photon, but to them, the photon still travels the straight path between them in time t, according to their clock. |
Now, we have formed a right triangle whose sides are formed by lines defining the apparent physical path of a photon between A and B as described from their point of view as opposed to the same path as defined from observer K, on the static ground plane, as they move past him in parallel at constant speed v relative to him. However, if they measured their speed relative to the ground, they would agree with observer K.
The speed v must be accounted for by observer K. Observers A and B
have no need to refer to it to define the photon path between them because they are relatively static to each other, so it is irrelevant to them and is not a necessary factor in their definition of the photon path.
Deriving Physical Interpretations From the Triangle
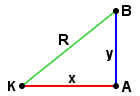 |
Based on the definition of the relativistic triangle given above, we will now proceed to derive the basic equations describing the relative physical
situation between the two frames of reference used by the observers to describe and compare their observations.
We are observing the motions as if looking down from an imaginary third dimension directly above a static, Euclidean ground plane. |
y = ct
Equation 1 |
Observers A and B are static relative to each other and separated by constant distance y over which the photon travels in time t, according to them. They make no reference to the static ground plane.
As long as they remain parallel at all times, the distance y has the same numerical value in both frames of reference, regardless of whether A and B are static or in parallel motion relative to the ground plane. This is true whether or not the speed is constant or accelerating.
The distance y is the apparent path of the photon as measured by both observers A and B relative to their local reference frames, which in this case, are one-in-the-same, so they can share a common synchronous clock for their local times. |
x = vT
Equation 2 |
Observers A
and B, traveling in parallel at constant speed v, as
measured relative to the static ground plane, span horizontal distance x
while the photon spans the vertical distance y between them in time t, according to them. |
R
= cT
Equation 3 |
From the ground
plane, the path R of the photon is measured along the green diagonal line.
This line combines the horizontal motion of A and B with
the vertical motion of the photon between them.
While the photon travels this path, A and B measure the time of this event as taking time t, while observer K measures the same event as taking time T. |
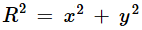
Equation 4 |
This
equation represents the Pythagorean theorem of right triangles,
which states that the square of the length of the hypotenuse (diagonal side)
is the sum of the squares of the other two sides.
This theorem can
now be applied to the sides of the relativistic right triangle defined
above, which leads to some interesting relationships. |
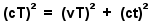
Equation 5 |
Substituting
the the respective triangle sides, in terms of the variables (v, c, t,
T), into equation 4, results in equation 5. |
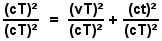
Equation 6 |
To
simplify equation 5 and transform it into a form that will more clearly
reveal the relationships between the variables, we can divide both sides through by the left member of the equation, putting it into the form of equation 6 and then reduce it by removing the common c and T factors which converts equation 6 into equation 7 below. |
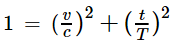
Equation 7 |
Upon
removing the common c and T factors from both sides of
equation 6, we arrive at equation 7.
This equation may be
recognized as an elliptical equation.
In this form, it more clearly shows the physical relationships between both frames of reference under the established conditions.
All observers would agree on the numerical values of v and c, but would differ in their measurements of t and T |
Now, from Equation 7, we may proceed to easily derive the specific
equations for interrelating each of the individual variables in terms of the
others. Doing so yields the following interesting results.
|
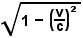
Equation 8
sometimes expressed as
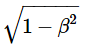
Equation 8a |
This
equation is the famous Lorentz contraction factor which is
commonly seen in relativistic formulations.
It gives the apparent time and/or distance contraction factor in the direction of motion of an object moving at speed v, according to a relatively static observer.
This value approaches zero as v approaches c.
It is also often encountered in the form of equation 8a, where the beta term represents the relativistic light speed ratio in the sense that 1.0 = the speed of light and a beta value of 0.567 means a speed of 56.7% of the speed of light. |
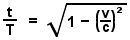
Equation 9 |
This
equation gives the ratio of a moving observer's time t to a relatively static rest frame observer's time T, while passing between two mutually agreed upon points in space, where the constant relative speed between the points is v. |
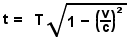
Equation 10 |
The time interval t of a moving observer, relative to the static rest frame in terms of constant relative speed v and rest frame time interval T, is given by this equation.
It states that a moving observer will experience less time while traveling between two mutually agreed upon points in space than a relatively static observer.
When the traveller and the relatively static observer compare travel times at the end of the trip, the traveller's clock will say that the trip took less time (t) than the time (T) that was measured by the static observer, even though they are both referring to the same event and used identical clocks to measure it, and without conflict with the observed 'laws' of nature or physics.
|
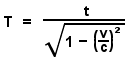
Equation 11 |
The time interval T of a static observer, relative to a moving observer, in terms of constant relative speed v and the moving observer's time interval t, may be determined by this equation.
It states that a relatively static observer will experience more time
than a moving observer traveling between two mutually agreed upon
points in space. It is the counterpart of equation 10.
|
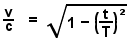
Equation 12 |
If
only the relative times between the two frames of reference are known,
equation 12 defines the relative constant speed v between them
while traveling between two mutually agreed upon points in space. |
| The formulas derived above are the basic essence of the Special Relativity
theory which have been experimentally verified to an extremely high
degree of precision. The special theory does not take accelerations into account. That is the domain of the general theory. |