This program computes the apparent angular diameter of a simple sphere at any distance from the eye as reckoned from the center or surface of the sphere.
The units are dimensionless, which means that
The default initial values are the mean radius of the moon and its mean geocentric distance from Earth, both in statute miles.
The units are dimensionless, which means that
5970 units can mean whatever you decide, such as 5970 miles, kilometers, feet, meters, etc., just as long as both the radius and distance use the same units.
The default initial values are the mean radius of the moon and its mean geocentric distance from Earth, both in statute miles.
The simple formulas defined below take into account the actual forward curvature of the spherical surface towards the eye and 3D perspective with respect to the eye point rather than treating the sphere as a flat circular disk of the same radius as viewed from a distance. This is extremely important when viewing a sphere from relatively not too far away, such as a planet or the lunar surface as viewed from a spacecraft only a few thousands of kilometers or miles away rather than hundreds of thousands or more.
Only for great distances from the eye, can we treat a sphere as a flat circular disk, but for much closer distances, we need to account for the perspective to obtain the correct angular diameter. The equations for this are actually quite simple and come from elementary trigonometry translated in a physical context.
Only for great distances from the eye, can we treat a sphere as a flat circular disk, but for much closer distances, we need to account for the perspective to obtain the correct angular diameter. The equations for this are actually quite simple and come from elementary trigonometry translated in a physical context.
 |
Where the Distance to the Eye is Reckoned From the Center of the Sphere:
Given the radius (R) of the sphere and the distance (D) to the eye point, as measured from the center of the sphere, the angular diameter $(\large\alpha)$ of the sphere as viewed from that point is:
$\Large{\alpha ~=~ 2\cdot cos^{-1}\left(\frac{\sqrt{D^2 ~-~ R^2}}{D}\right)}$ Where: $R > 0$ and $D > R$ |
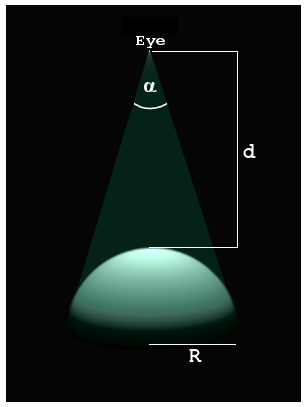 |
Where the Distance to the Eye is Reckoned From the Surface of the Sphere:
Given the radius (R) of the sphere and the distance (d) to the eye point, as measured from the surface, the general equation for the angular diameter $(\large\alpha)$ of the sphere as viewed from that point is:
$\Large{\alpha ~=~ 2\cdot cos^{-1}\left(\frac{\sqrt{d^2 ~+~ 2Rd}}{R ~+~ d}\right)}$ Where: $R > 0$ and $d > 0$ |
© 2025 - Jay Tanner - v3.5