Distance From Eye to Horizon of a Sphere
This program computes the line-of-sight distance and the curved surface distance to the horizon of a sphere at any distance of the eye as reckoned from the surface or center of the sphere. The radius and distance can be in any convenient linear units.The initial defaults radius is the mean lunar radius and the distance is 1/100th of the mean geocentric distance of the eye from the center of the moon, both in statute miles.
Line-of-Sight Distance (H) to Horizon =
2131.2729945974Surface Distance (S) to Horizon =
1189.4592885523The distance
(D) to the eye is reckoned from the center of the sphere.
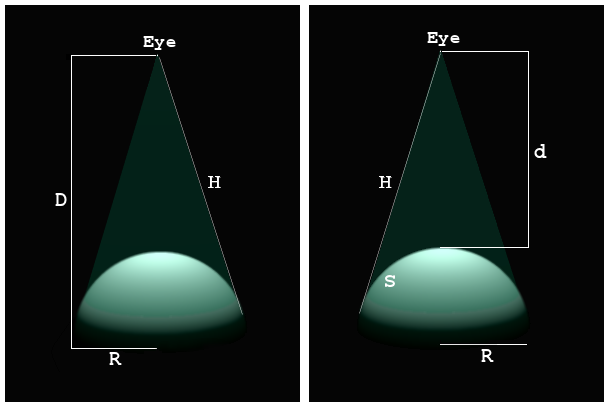
Where the Distance to the Eye Is Reckoned From the Center of the Sphere:
Given the radius (
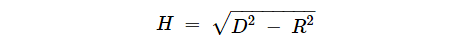
The horizon surface distance
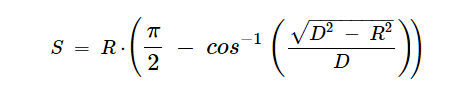
Given the radius (
R) of the sphere and the distance (D) of the eye from the center of the sphere, the general equation for the line-of-sight distance (H) to the sphere horizon viewed from that point is:
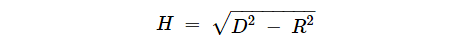
The horizon surface distance
(S), corresponding to (H), but measured along the curved surface of the sphere directly below H and corresponding to the sailing distance is:
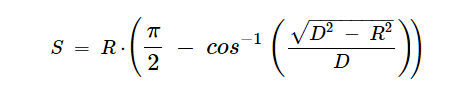
Where: D > R and R > 0 and the inverse angle is expressed in radians
Where the Distance to the Eye Is Reckoned From the Surface of the Sphere:
Given the radius ( height) of the eye above the surface of the sphere, the general equation for the line-of-sight distance

The horizon surface distance
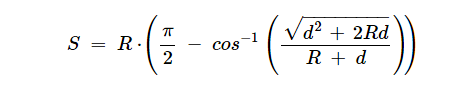
(R) of the sphere and the distance (d) (H) to the sphere horizon viewed from that point is:

The horizon surface distance
(S), corresponding to line-of-sight distance (H), but measured along the curved surface of the sphere, corresponding to the sailing distance is:
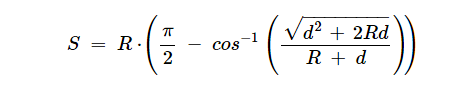
Where: R > 0 and d > 0 and the inverse angle is expressed in radians
© Jay Tanner - 2025 - v2.0