The Basic Mathematics Of The Stellar Magnitude System
Generally, stellar magnitude refers to the apparent brightness of an astronomical object. The brightness magnitude system applied to the stars is also applied to other astronomical objects such as planets, comets, nebulae, galaxies and even the sun and moon.
The Basic Mathematics Of The Stellar Magnitude Ranking System
Stellar magnitude 3 is fainter than magnitude 1, which may seem odd at first glance. This is because stellar brightness is generally measured in units referred to as magnitudes, which are analogous to ranks.
1st magnitude is to 3rd magnitude as 1st prize is to 3rd prize. This is why magnitude 1 is brighter than magnitude 3 and magnitude 0 is even brighter than magnitude 1 and magnitude −1 is even brighter yet!
Given a set of stellar magnitudes, the object with the greatest numerical value is always the faintest of the set and the lowest magnitude value indicates the brighest object. Negative magnitudes always indicate very bright objects, for example, sun at -26.74, the full moon at -12.5, or Venus at -4.5, etc. An asteroid may have a magnitude such as +10, which is very faint and Pluto even fainter at magnitude +14, which is extremely faint. For comparison, the star Vega (alpha Lyrae) is often cited as a general example of a star of 0 (zero) magnitude.
Here, the distances to the stars can be ignored. We do not need to think about the distances when simply ranking stars by their relative apparent brightness in the sky as we see them from Earth. However, when we start to move around in space or compare stars to each other, as if side-by-side, then we will have to consider their distances too.
The stellar magnitude system is designed mathematically so that a difference of exactly 5 magnitudes equates to an apparent brightness ratio (b) of exactly 100-fold. It is a base-10 logarithmic system of astronomical brightness scaling analogous to the Richter or decibel scales used to measure energy intensity.
The general relationship between apparent difference in magnitude vs apparent ratio in brightness may be expressed by the simple equation
A Numerical Example of Computing the Brightness Ratio Between Two Objects
Given the apparent magnitudes of two astronomical objects (e.g, stars, planets, etc.), Equation 1 computes their comparative brightness ratio.
Let:
m1 = +0.068 = Magnitude of brighter object
and
m2 = +5.745 = Magnitude of fainter object
The brightness ratio (b) between the brighter and fainter objects is:
brighter than the object of magnitude
Combining the Magnitudes of Two or More Stars Into a Single Magnitude Value
To the naked eye what may appear to be a single star may in fact be two or more stars very close together or apparently so due to the line of sight. Several double and multiple star systems appear as a single star to the unaided eye, so what we actually see is the sum of their combined magnitudes.
In general, if there are two or more stars, then the singular combined magnitude value can be found from the following equation.
Let
M = Singular magnitude of N stars combined into one
mn = Magnitude of nth star of a group of N stars, taken in any order
The general formula for N combined stellar magnitudes may be expressed as:
Apparent Magnitude With Respect to Distance
Having covered the general relationship between apparent magnitude and brightness, we can now proceed to the next step and add distance to the problem. Using the following equations, we can mathematically move a star around in space and compute its apparent brightness at any given distance from any given known starting values.
This also allows us to mathematically compare the relative brightness of any two stars side-by-side at any common distance. For example, how bright a star would our sun appear to be if viewed from the same distance as Alpha Centauri? Or how bright would Alpha Centauri appear to be if it replaced our sun?
Let
m1 = Apparent magnitude of a star at distance d1
m2 = Apparent magnitude of the same star at distance d2
Distances can be in any convenient, consistent units, such as AUs, light years, etc.
The relationship between apparent magnitude and distance may be expressed in terms of any of the four variables as in the following equations.
The Basic Mathematics Of The Stellar Magnitude Ranking System
Stellar magnitude 3 is fainter than magnitude 1, which may seem odd at first glance. This is because stellar brightness is generally measured in units referred to as magnitudes, which are analogous to ranks.
1st magnitude is to 3rd magnitude as 1st prize is to 3rd prize. This is why magnitude 1 is brighter than magnitude 3 and magnitude 0 is even brighter than magnitude 1 and magnitude −1 is even brighter yet!
Given a set of stellar magnitudes, the object with the greatest numerical value is always the faintest of the set and the lowest magnitude value indicates the brighest object. Negative magnitudes always indicate very bright objects, for example, sun at -26.74, the full moon at -12.5, or Venus at -4.5, etc. An asteroid may have a magnitude such as +10, which is very faint and Pluto even fainter at magnitude +14, which is extremely faint. For comparison, the star Vega (alpha Lyrae) is often cited as a general example of a star of 0 (zero) magnitude.
Here, the distances to the stars can be ignored. We do not need to think about the distances when simply ranking stars by their relative apparent brightness in the sky as we see them from Earth. However, when we start to move around in space or compare stars to each other, as if side-by-side, then we will have to consider their distances too.
The stellar magnitude system is designed mathematically so that a difference of exactly 5 magnitudes equates to an apparent brightness ratio (b) of exactly 100-fold. It is a base-10 logarithmic system of astronomical brightness scaling analogous to the Richter or decibel scales used to measure energy intensity.
The general relationship between apparent difference in magnitude vs apparent ratio in brightness may be expressed by the simple equation
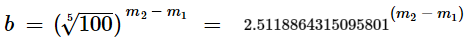
Eq. 1
A Numerical Example of Computing the Brightness Ratio Between Two Objects
Given the apparent magnitudes of two astronomical objects (e.g, stars, planets, etc.), Equation 1 computes their comparative brightness ratio.
Let:
m1 = +0.068 = Magnitude of brighter object
and
m2 = +5.745 = Magnitude of fainter object
The brightness ratio (b) between the brighter and fainter objects is:
dm = (m2 − m1) = (+5.745 − +0.068) = 5.677 b = 2.5118864315095801 ^ 5.677 = 186.552039This means that the object with magnitude
+0.068 is about 187 timesbrighter than the object of magnitude
+5.745
Combining the Magnitudes of Two or More Stars Into a Single Magnitude Value
To the naked eye what may appear to be a single star may in fact be two or more stars very close together or apparently so due to the line of sight. Several double and multiple star systems appear as a single star to the unaided eye, so what we actually see is the sum of their combined magnitudes.
In general, if there are two or more stars, then the singular combined magnitude value can be found from the following equation.
Let
M = Singular magnitude of N stars combined into one
mn = Magnitude of nth star of a group of N stars, taken in any order
The general formula for N combined stellar magnitudes may be expressed as:
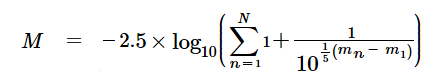
Eq. 2
Apparent Magnitude With Respect to Distance
Having covered the general relationship between apparent magnitude and brightness, we can now proceed to the next step and add distance to the problem. Using the following equations, we can mathematically move a star around in space and compute its apparent brightness at any given distance from any given known starting values.
This also allows us to mathematically compare the relative brightness of any two stars side-by-side at any common distance. For example, how bright a star would our sun appear to be if viewed from the same distance as Alpha Centauri? Or how bright would Alpha Centauri appear to be if it replaced our sun?
Let
m1 = Apparent magnitude of a star at distance d1
m2 = Apparent magnitude of the same star at distance d2
Distances can be in any convenient, consistent units, such as AUs, light years, etc.
The relationship between apparent magnitude and distance may be expressed in terms of any of the four variables as in the following equations.

Eq. 3

Eq. 4
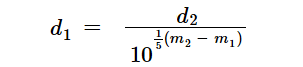
Eq. 5

Eq. 6
© Jay Tanner - PHP Science Labs - 2025